每日算法(四)数组

按要求打印数组

转圈打印矩阵

题目:

思路：

利用对角进行打印

public static void spiralOrderPrint(int[][] matrix) {
		// 左上角
		int tR = 0;
		int tC = 0;
		// 右底角
		int dR = matrix.length - 1;
		int dC = matrix[0].length - 1;
		while (tR <= dR && tC <= dC) {
			printEdge(matrix, tR++, tC++, dR--, dC--);
		}
	}

	public static void printEdge(int[][] m, int tR, int tC, int dR, int dC) {
      // 处于同一行
		if (tR == dR) { 
			for (int i = tC; i <= dC; i++) {
				System.out.print(m[tR][i] + " ");
			}
          // 处于同一列
		} else if (tC == dC) { 
			for (int i = tR; i <= dR; i++) {
				System.out.print(m[i][tC] + " ");
			}
		} else { 
          // 正常打印
			int curC = tC;
			int curR = tR;
			while (curC != dC) {
				System.out.print(m[tR][curC] + " ");
				curC++;
			}
			while (curR != dR) {
				System.out.print(m[curR][dC] + " ");
				curR++;
			}
			while (curC != tC) {
				System.out.print(m[dR][curC] + " ");
				curC--;
			}
			while (curR != tR) {
				System.out.print(m[curR][tC] + " ");
				curR--;
			}
		}
	}

正方形矩阵顺时针打印

题目:

给定一个N×N的矩阵 matrIx，把这个矩阵调整成顺时针转动90°后的形式

思路:

还是利用左上角和右下角观察到转动90° 就是移动左上角的横坐标和右底角的纵坐标的差

public static void rotate(int[][] matrix) {
		int tR = 0;
		int tC = 0;
		int dR = matrix.length - 1;
		int dC = matrix[0].length - 1;
		while (tR < dR) {
			rotateEdge(matrix, tR++, tC++, dR--, dC--);
		}
	}

	public static void rotateEdge(int[][] m, int tR, int tC, int dR, int dC) {
		int times = dC - tC; // 右底角 - 左上角
		int tmp = 0;
      // 交换
		for (int i = 0; i != times; i++) { 
			tmp = m[tR][tC + i];
			m[tR][tC + i] = m[dR - i][tC];
			m[dR - i][tC] = m[dR][dC - i];
			m[dR][dC - i] = m[tR + i][dC];
			m[tR + i][dC] = tmp;
		}
	}

之字型打印矩阵

题目:

给定一个矩阵 matrIx，按照“之”字形的方式打印这个矩阵，例如

1 2 3 4

5 6 7 8

9 10 11 12

打印结果为1,2,5,9,6,3,4,7,10,11,8,12

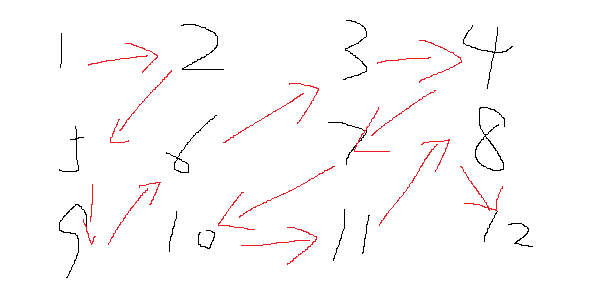
思路:

两个点开始都在(0,0) A往右移动再往下移动 B往下移动再往右移动

	public static void printMatrixZigZag(int[][] matrix) {
		int tR = 0;
		int tC = 0;
		int dR = 0;
		int dC = 0;
		// 终点
		int endR = matrix.length - 1;
		int endC = matrix[0].length - 1;
		// 打印方向
		boolean fromUp = false;
		// 没到终点
		while (tR != endR + 1) {
			printLevel(matrix, tR, tC, dR, dC, fromUp);
			tR = tC == endC ? tR + 1 : tR;
			tC = tC == endC ? tC : tC + 1;
			dC = dR == endR ? dC + 1 : dC;
			dR = dR == endR ? dR : dR + 1;
			fromUp = !fromUp;
		}
		System.out.println();
	}

	public static void printLevel(int[][] m, int tR, int tC, int dR, int dC,
			boolean f) {
			// 左下->右上
		if (f) {
			while (tR != dR + 1) {
				System.out.print(m[tR++][tC--] + " ");
			}
			// 右上->左下
		} else {
			while (dR != tR - 1) {
				System.out.print(m[dR--][dC++] + " ");
			}
		}
	}

未排序数组中累加和问题

未排序正数数组中累加和为给定值的最长子数组长度

题目:

给定一个数组arr，该数组无序，但每个值均为正数，再给定一个正数k。求ar的所有子数组中所有元素相加和为k的最长子数组长度

思路: 滑动窗口

 public static int getMaxLength(int[] arr, int k) {
        if (arr == null || arr.length == 0 || k < 1) return -1;
        int left = 0;
        int right = 0;
        int len = 0;
        int sum = arr[0];
        while (right < arr.length) {
          // 相等 记录此时长度 继续往后遍历
            if (sum == k) {
                len = Math.max(len, right - left + 1);
                sum -= arr[left++];
              // 小于 right往右扩一位
            } else if (sum < k) {
                right++;
                if (right == arr.length) break;
                sum += arr[right];
            } else {
              // 大于 left往右扩一位
                sum -= arr[left++];
            }
        }
        return len;
    }
// 时间复杂度 O(N)  空间复杂度 O(1)

未排序数组中累加和为给定值的最长子数组长度

题目:

给定一个数组arr，该数组无序，每个值可正可负可0，再给定一个整数k。求ar的所有子数组中所有元素相加和为k的最长子数组长度

思路:

arr[j+1,i]: 的累计和为s(i) - (j) 并且应该从-1位置开始考虑

sum: 从0位置一直加到i位置所有元素的和
len: 累加和为k的最长子数组长度
map:
- key: 从arr最左边开始累加的过程中出现过的sum值
- value: sum值最早出现的位置

map.put(0,-1)

意义在于一个数也不加时累加和为0 且位置为 - 1

例如 [ 1, 2, 3, 3] k = 6

遍历到第一个3 此时是 sum = 6 map : key 1 : value 0 key3 : value 1

map.get (sum - k) 没有值则 [1,2,3]被忽略

若加了则长度是 2 - (- 1) = 3

public int maxLength(int[] arr,int k){
        if(arr == null || arr.length == 0 ||  k < 1) return -1;
        HashMap<Integer,Integer> map = new HashMap<>();
        // 重要
        map.put(0,-1);
        int len = 0;
        int sum = 0;
        for(int i = 0; i != arr.length;i++){
            sum += arr[i];
            if(map.containsKey(sum - k)){
                len = Math.max(i - map.get(sum - k),len);
            }
            if(!map.containsKey(sum)){
                map.put(sum,i);
            }
        }
        return len;
    }

未排序数组中累加和小于或等于给定值的最长子数组长度

题目:

给定一个无序数组arr，其中元素可正、可负、可0，给定一个整数k。求ar所有的子数组中累加和小于或等于k的最长子数组长度

思路:

求以0~j位置的累加和sum[0,j] 以j结尾的相加小于等于k的最长子数组要得到大于等于sum[0,j] - k 出现在什么位置假如为i 则区间为arr[i + 1,j]

sumArr : 从左到右的累加和数组 sumArr 第一个数为0
helpArr: sumar的左侧最大值数组

public static int maxLength(int[] arr, int k) {
		int[] h = new int[arr.length + 1];
		int sum = 0;
		h[0] = sum;
  // 生成helpArr数组
		for (int i = 0; i != arr.length; i++) {
			sum += arr[i];
			h[i + 1] = Math.max(sum, h[i]);
		}
		sum = 0;
		int res = 0;
		int pre = 0;
		int len = 0;
  //遍历查找数组 满足大于等于sum[0,j] - k 出现在什么位置 记录长度
		for (int i = 0; i != arr.length; i++) {
			sum += arr[i];
			pre = getLessIndex(h, sum - k);
			len = pre == -1 ? 0 : i - pre + 1;
			res = Math.max(res, len);
		}
		return res;
	}

// 二分查找出 大于等于num的位置
	public static int getLessIndex(int[] arr, int num) {
		int low = 0;
		int high = arr.length - 1;
		int mid = 0;
		int res = -1;
		while (low <= high) {
			mid = (low + high) / 2;
			if (arr[mid] >= num) {
				res = mid;
				high = mid - 1;
			} else {
				low = mid + 1;
			}
		}
		return res;
	}

子数组的最大累加和问题

题目:

给定一个数组arr，返回子数组的最大累加和

思路:

要求是返回最大累加和而不是长度就没必要用滑动窗口对于负数直接归为0即可这样能保证是最大的

public static int maxSum(int[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		int max = Integer.MIN_VALUE;
		int cur = 0;
		for (int i = 0; i != arr.length; i++) {
			cur += arr[i];
			max = Math.max(max, cur);
          // 小于0 直接归0
			cur = cur < 0 ? 0 : cur;
		}
		return max;
	}

子矩阵的最大累加和问题

题目:

给定一个矩阵 matrIx，其中的值有正、有负、有0，返回子矩阵的最大累加和

思路:

利用上面一题的子数组判定一个数组的最大累加和矩阵从第一行..最后一行开始累加求值再第二行…最后一行

public static int maxSum(int[][] m) {
		if (m == null || m.length == 0 || m[0].length == 0) {
			return 0;
		}
		int max = Integer.MIN_VALUE;
		int cur = 0;
		int[] s = null; 
  // 从第几行开始累加 
		for (int i = 0; i != m.length; i++) {
			s = new int[m[0].length];
          // 第几行
			for (int j = i; j != m.length; j++) {
				cur = 0;
              //第几列
				for (int k = 0; k != s.length; k++) {
					s[k] += m[j][k];
					cur += s[k];
					max = Math.max(max, cur);
					cur = cur < 0 ? 0 : cur;
				}
			}
		}
		return max;
	}
// 时间复杂度O(N^3)  空间复杂度 O(N)

数组中子数组的最大累乘积

题目:

给定一个 double类型的数组ar，其中的元素可正、可负、可0，返回子数组累乘的最大乘积

思路:

假设以arr[i-1]尾的最小累乘积为min，以arr[i-1]结尾的最大累乘积为max。那么，以arri结尾的最大累乘积只有以下三种可能

max * arr[i] : [1 ,2 ,3]
min * arr[i] : [-1,2,-3]
arr[i] : [0,1,2]

public static double maxProduct(double[] arr) {
		if (arr == null || arr.length == 0) {
			return 0;
		}
		double max = arr[0];
		double min = arr[0];
		double res = arr[0];
		double maxEnd = 0;
		double minEnd = 0;
		for (int i = 1; i < arr.length; ++i) {
			maxEnd = max * arr[i];
			minEnd = min * arr[i];
			max = Math.max(Math.max(maxEnd, minEnd), arr[i]);
			min = Math.min(Math.min(maxEnd, minEnd), arr[i]);
			res = Math.max(res, max);
		}
		return res;
	}
// 时间复杂度 O(N) 空间复杂度 O(1)

小结

滑动窗口

设置两个指针 left right 满足条件时 right 向右扩一位不满足时left 向右阔一位可以利用一个变量max 去记录最大值什么的

每日算法(四) 数组

目录