目录
每日算法(三)—-动态规划
给定一个数字三角形,找到从顶部到底部的最小路径和。每一步可以移动到下面一行的相邻数字上
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
// 最小路径: 2 + 3 + 5 + 1 = 11
遍历法
void traverse(int x, int y, int sum){
// sum是走到当前 x y 点的时候 路径的和 不包括x y
if(x == n){
if(sum<best){
best = sum;
}
return;
}
traverse(x+l,y+l,sum + A[x][y]);
traverse(x + 1,y,sum + A[x][y]);
}
traverse(0,0,0);
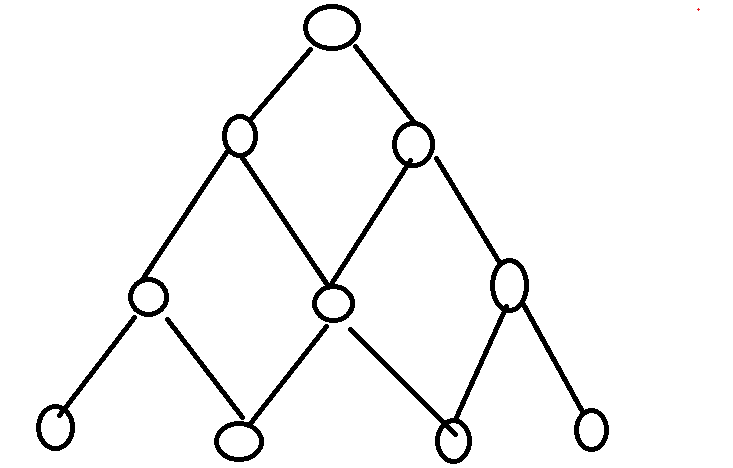
代码遍历 如上图 中间的结点走了2次 N为结点的个数 n为上面的图的高度
时间复杂度: 根据代码来看 每次在前面有2条路径 又有n层 于是时间复杂度为O(2 ^ n)
分治法
int dfs(int x,int y){
if(x == n)return 0;
return A[x][y]+ Math.min(dfs(x+1,y),dfs(x + 1, y + 1));
}
dfs(0,0);
时间复杂度同样是 O(2 ^ n)
分治 + 记忆化搜索
int dfs(int x, int y ){
if(x == n) return 0;
if(hash[x][y] != Integer.MAX_VALUE){
return hash[x][y];
}
hash[x][y] = A[x][y] + Math.min(dfs(x + 1 ,y),dfs(x + 1,y + 1));
return hash[x][y];
}
hash[*][*] = Integer.MAX_VALUE;
dfs(0,0);
时间复杂度: O(n ^ 2)
多重循环
- 自底向上
A[][]
// 状态定义 表示从i,j出发走到最后一层的最小路径长度
f[i][j]
// 初始化 从最底下开始赋值
for(int i = 0;i < n;i++){
f[n - 1][i] = A[n - 1][i];
}
// 循环递推求解
for(int i = n - 2; i >= 0; i--){
for(int j = 0;j <= i; j++){
// 选择左边和右边的最小值
f[i][j] = Math.min(f[i + 1][j], f[i + 1][j + 1]) + A[i][j];
}
}
// 求最终的结果 起点
f[0][0]
时间复杂度: O(n ^ 2)
- 自顶向下
// 初始化: 起点
f[0][0] = A[0][0]
// 初始化3角形的左边和右边 边缘
for(int i = 1; i < n; i++){
f[i][0] = f[i - 1][0] + A[i][0];
f[i][i] = f[i - 1][i - 1] + A[i][i];
}
// 循环递推求解
for(int i = 1; i < n;i--){
for(int j = 1; j < i;j++){
f[i][j] = Math.min(f[i - 1][j],f[i - 1][j - 1]) + A[i][j];
}
}
Math.min(f[n - 1][0], f[n - 1][1], f[n - 1][2]..);
多重循环 VS 记忆化搜索
- 多重循环:
- 优点:正规,大多数面试官可以接受,存在空间优化可能性
- 缺点:思考有难度
- 记忆化搜索:
- 优点: 容易从搜索算法直接转化过来 有的时候可以节省更多的时间
- 缺点: 递归
什么时候使用动态规划
- 求最大值最小值
- 判断是否可行
- 统计方案个数 而不是具体方案
如何使用动态规划
f[][] : 定义好状态
初始化
方程
答案
常见动态规划类型
坐标型动态规划
state f【×】表示我从起点走到坐标x…
f【×】【y】表示我从起点走到坐标x,y…
function:研究走到x,y这个点之前的一步
intialize:起点
answer:终点
最小路径和
给定一个只含非负整数的m*n网格,找到一条从左上角到右下角的可以使数字和最小的路径 只能向右 或向下
// f[x][y]: 到 x y 的路径数字和
public int minPathSum(int[][] grid) {
if (grid == null || grid.length == 0 || grid[0].length == 0) {
return 0;
}
int M = grid.length;
int N = grid[0].length;
int[][] sum = new int[M][N];
sum[0][0] = grid[0][0];
for (int i = 1; i < M; i++) {
sum[i][0] = sum[i - 1][0] + grid[i][0];
}
for (int i = 1; i < N; i++) {
sum[0][i] = sum[0][i - 1] + grid[0][i];
}
for (int i = 1; i < M; i++) {
for (int j = 1; j < N; j++) {
sum[i][j] = Math.min(sum[i - 1][j], sum[i][j - 1]) + grid[i][j];
}
}
return sum[M - 1][N - 1];
}
}
单序列动态规划
state: f[i] 表示前i个位置/数字/字母,
function:f[i]=f[j]… j是i之前的一个位置
initialize:f[0]..
answer:f[n - 1]..
单序列动态规划没有坐标的概念 但有子串 前缀串的关系
区别是 因为考虑了前i 开辟数组的时候 就要开辟n +1个数
分割回文串 ||
// state: f[i] 前 i 个字符组成的子字符串最少需要cut 几次
假如在 j 和 j + 1那儿进行切分 则要判断在j +1 和 i之间是否是回文串 是回文串 则切 j ~ j + 1之间就时产生一个候选方案 就可以表示为f[i]+1 但只是候选方案 不是一定的 因为 j 可以变动 即0 ~ i - 1 如下图 可以在任意之间分割 去尝试
// function:
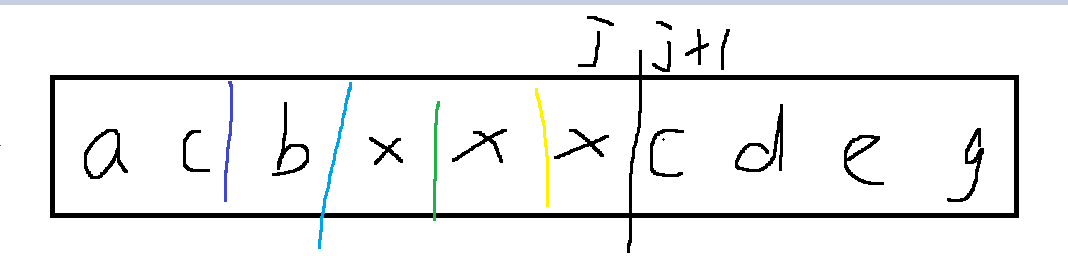
// 根据上面的分析 得出这个
for(int i = 1; i <=s.length();i++){
// 0 ~ i - 1之间插入
for(int j = 0; j < i;j++){
if(isPalindrome[j][i-1]){
f[i] = Math.min(f[i], f[j] + 1);
}
}
}
预处理
f[i][j] : i -> j范围内是否是回文
// axxxxa i 是前面最右边的x j 是最左边的x
f[i][j] = f[i + 1][j - 1] && s[i] == s[j]
// 不能用for(int i:0 -> n) 得从大到小
// 因为大区间 依赖小区间 所以要先算小区间的长度 然后再去循环起始位置
// getIsPalindrome(String s): 使用的是区间型dp
private boolean[][] getIsPalindrome(String s) {
boolean[][] isPalindrome = new boolean[s.length()][s.length()];
for(int i = 0 ; i < s.length();i++){
isPalindrome[i][i] = true;
}
for(int i = 0; i< s.length() - 1;i++){
isPalindrome[i][i + 1] = (s.charAt(i) == s.charAt(i + 1));
}
for(int length = 2; length < s.length();length++){
for(int start = 0; start + length < s.length(); start++){
isPalindrome[start][start + length]
= isPalindrome[start + 1][start + length - 1 ] && s.charAt(start) == s.charAt(start + length);
}
}
return isPalindrome;
}
初始化
// 3个字符划2刀 这样每个地方就是回文串 于是i个字符 划1 - 1刀 就能得到回文字符串
int[] f = new int[s.length() + 1];
for (int i = 0; i <= s.length(); i++) {
f[i] = i - 1;
}
public int minCut(String s) {
if (s == null || s.length() == 0) return 0;
// 预处理
boolean[][] isPalindrome = getIsPalindrome(s);
// 初始化
int[] f = new int[s.length() + 1];
for (int i = 0; i <= s.length(); i++) {
f[i] = i - 1;
}
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i; j++) {
if (isPalindrome[j][i - 1]) {
f[i] = Math.min(f[i], f[j] + 1);
}
}
}
return f[s.length()];
}
如果不是跟坐标相关的动态规划般有N个数/字符,就开N+1个位置的数组第0个位置单独留出来作初始化
word break
// state: f[i]: 前 i 个字符能否被完美切分
// function: f[i] = OR{f[j]} , j < i, j + 1 ~ i是词典的单词
// f[i] = f[j] && j + 1 ~ i 在dict中
// initialize: f[0] = true
// answer : f[s.length()]
public class Solution {
private int getMaxLength(Set<String> dict) {
int maxLength = 0;
for (String word : dict) {
maxLength = Math.max(maxLength, word.length());
}
return maxLength;
}
public boolean wordBreak(String s, Set<String> dict) {
if (s == null || s.length() == 0) {
return true;
}
int maxLength = getMaxLength(dict);
boolean[] canSegment = new boolean[s.length() + 1];
canSegment[0] = true;
for (int i = 1; i <= s.length(); i++) {
canSegment[i] = false;
// 开始切 单词长度不能大于最长的 且切割的不能
for (int lastWordLength = 1;
lastWordLength <= maxLength && lastWordLength <= i;
lastWordLength++) {
if (!canSegment[i - lastWordLength]) {
continue;
}
String word = s.substring(i - lastWordLength, i);
// 这里算上单词长度的话 就是L
if (dict.contains(word)) {
canSegment[i] = true;
break;
}
}
}
return canSegment[s.length()];
}
}
// 时间复杂度 O(N * L ^ 2) N:字符串长度L:最长的单词的长度
双序列动态规划
// state: f[i][j]代表了第一个 sequence的前i个数字/字符,配上第二个 sequence的前j个
// function: f[i][j] = 研宄第个和第j个的匹配关系
// initialize: f[i][0]和f[0][j]
// answer: f[s1.length()][s2.length()]
Longest Common Subsequence
// state: f[i][j] 表示前i个字符配上前j个字符的LCS的长度
// function: f[i][j]
= MAX(f[i - 1][j],f[i][j - 1],f[i - 1][j - 1] + 1 ) // a[i]==b[j]
= MAX(f[i - 1][j],f[i][j - 1]) // a[i] != b[j]
// f[i - 1][j] // 让J的a和i的前面的a匹配
i: abcd a x
\
j: edfg z a
// intialize : f[i][0] = 0 f[0][i] = 0
// answer: f[a.length()][b.length()]
public int longestCommonSubsequence(String A, String B) {
int n = A.length();
int m = B.length();
int f[][] = new int[n + 1][m + 1];
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
f[i][j] = Math.max(f[i - 1][j], f[i][j - 1]);
if(A.charAt(i - 1) == B.charAt(j - 1))
f[i][j] = f[i - 1][j - 1] + 1;
}
}
return f[n][m];
}