操作系统之页面置换算法(三)

发生缺页中断时 OS需要在内存选择一个页面将其换出内存用来为调入的页面腾出空间如果要换出的页面修改过则需要回写磁盘否则直接覆盖该页面就行若一个频繁使用的页面被换出则很有可能又在不久被调入内存造成不必要开销因此需要合适的页面置换算法来决定调入到哪个页面

缺页次数 = 总数 - 空白列数

缺页率 = 缺页次数 / 总列数

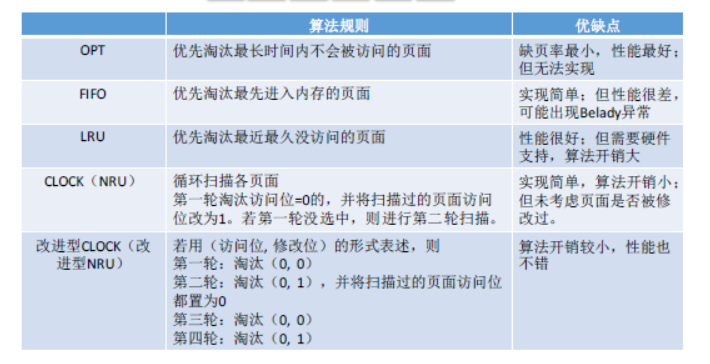
最佳置换算法(OPT)

每次选择淘汰的页面将是以后永不使用，或者在最长时间内不再被访问的页面，这样可以保证最低的缺页率。

它的前提是要预先知道所有要访问的页面, 但只有在进程执行的时候才能知道接下来会访问到哪个页面因此是无法实现的

先进先出算法 (FIFO)

每次选择淘汰的页面是最早进入内存的页面

实现方法：把调入内存的页面根据调入的先后顺序排成一个队列，需要换出页面时选择队头页面即可。

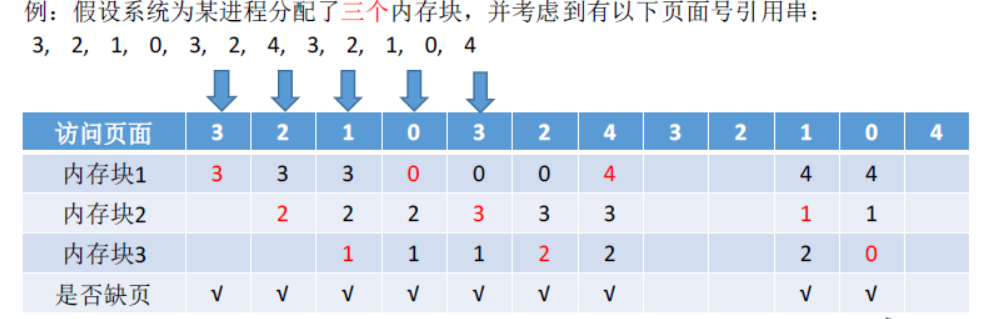
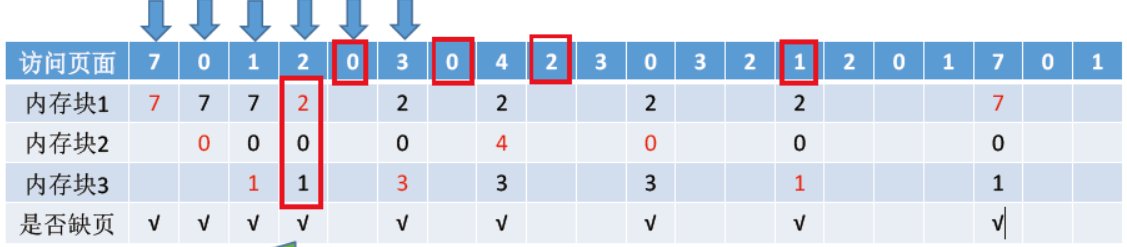
可以看为淘汰页面号最长的到0的时候 3页面号最长 于是淘汰3号上面总共缺页9次

FIFO 是唯一一个会产生Belady异常的算法即当当为进程分配的物理块数增大时，缺页次数不减反增的异常现象。

实现简单但考虑到实际运行情况的规律与该算法不一定适应先进入的页面也有可能被经常访问算法性能差

最近最久未使用置换算法 (LRU)

每次淘汰的页面是最近最久未使用的页面

实现方法：赋予每个页面对应的页表项中，用访问字段(下图)记录该页面自上次被访问以来所经历的时间t 当需要淘汰一个页面时，选择现有页面中t值最大的，即最近最久未使用的页面

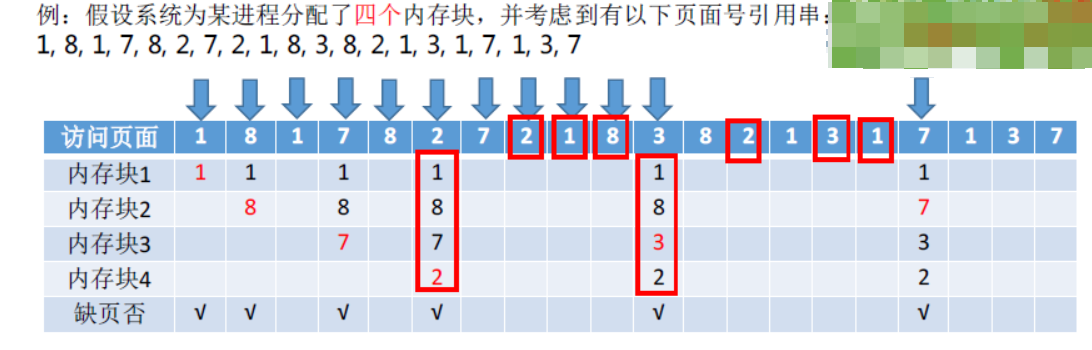
要访问3页面的时候从右往左推 发现7离3最远于是覆盖7

需要专门的硬件支持，虽然算法性能好但是实现围难，开销大


public class LRU {

    public static class Node<V> {
        public V value;
        public Node<V> last;
        public Node<V> next;

        public Node(V value) {
            this.value = value;
        }
    }

    public static class NodeDoubleLinkedList<V> {
        private Node<V> head;
        private Node<V> tail;

        public NodeDoubleLinkedList() {
            this.head = null;
            this.tail = null;
        }

        public void addNode(Node<V> newNode) {
            if (newNode == null) {
                return;
            }
            if (this.head == null) {
                this.head = newNode;
                this.tail = newNode;
            } else {
                this.tail.next = newNode;
                newNode.last = this.tail;
                this.tail = newNode;
            }
        }

        public void moveNodeToTail(Node<V> node) {
            // 本来就在最后面 不动
            if (this.tail == node) {
                return;
            }
            // 如果是在第一个 直接
            if (this.head == node) {
                this.head = node.next;
                this.head.last = null;
            } else {
                // 否则让该node断开
                node.last.next = node.next;
                node.next.last = node.last;
            }
            // 放入最后一个
            node.last = this.tail;
            node.next = null;
            this.tail.next = node;
            this.tail = node;
        }

        public Node<V> removeHead() {
            if (this.head == null) {
                return null;
            }
            Node<V> res = this.head;
            if (this.head == this.tail) {
                this.head = null;
                this.tail = null;
            } else {
                this.head = res.next;
                res.next = null;
                this.head.last = null;
            }
            return res;
        }

    }

    public static class MyCache<K, V> {
        private HashMap<K,Node<V>> keyNodeMap;
        private HashMap<Node<V>,K> nodeKeyMap;
        private NodeDoubleLinkedList<V> nodeList;
        private int capacity;

        public MyCache(int capacity) {
            if (capacity < 1) {
                throw new RuntimeException("should be more than 0.");
            }
            this.keyNodeMap = new HashMap<K, Node<V>>();
            this.nodeKeyMap = new HashMap<Node<V>, K>();
            this.nodeList = new NodeDoubleLinkedList<V>();
            this.capacity = capacity;
        }

        public V get(K key){
            if(this.keyNodeMap.containsKey(key)){
                Node<V> res = this.keyNodeMap.get(key);
                this.nodeList.moveNodeToTail(res);
                return res.value;
            }
            return null;
        }

        public void set(K key, V value){
            if(this.keyNodeMap.containsKey(key)){
                Node<V> node = this.keyNodeMap.get(key);
                node.value = value;
                this.nodeList.moveNodeToTail(node);
            }else{
                Node<V> newNode = new Node<>(value);
                this.keyNodeMap.put(key,newNode);
                this.nodeKeyMap.put(newNode, key);
                this.nodeList.addNode(newNode);
                // 超过了限制 则将最近醉久未使用的Node删除
                if(this.keyNodeMap.size() == this.capacity + 1){
                    this.removeMostUnusedCache();
                }
            }
        }
        private void removeMostUnusedCache(){
            Node<V> removeNode = this.nodeList.removeHead();
            K removeKey = this.nodeKeyMap.get(removeNode);
            this.nodeKeyMap.remove(removeNode);
            this.keyNodeMap.remove(removeKey);
        }
    }

    public static void main(String[] args) {
        MyCache<String, Integer> testCache = new MyCache<String, Integer>(3);
        testCache.set("A", 1);
        testCache.set("B", 2);
        testCache.set("C", 3);
        System.out.println(testCache.get("B"));
        System.out.println(testCache.get("A"));
        testCache.set("D", 4);
        System.out.println(testCache.get("D"));
        System.out.println(testCache.get("C"));
    }
}

时钟置换算法(CLOCK)

为每个页面设置一个访问位，再将内存中的页面都通过链接指针链接成个循环队列。形似时钟当某页被访问时，其访问位置为1.当需要淘汰一个页面时，只需检查页的访问位如果是0，就选择该页换出；如果是1，则将它置为0，暂不换出，继续检査下一个页面，若第一轮扫描中所有页面都是1，则将这些页面的访问位依次置为0后，再进行第二轮扫描（第二轮扫描中一定会有访问位为0的页面，因此简单的 CLOCK算法选择一个淘汰页面最多会经过两轮扫描）

如果访问位为0 淘汰为1 则置为0 访问下一个

改进型的时钟置换算法

简单的时钟置换算法仅考虑到一个页面最近是否被访问过。事实上，如果被淘汰的页面没有被修改过，就不需要执行I/O操作写回外存。只有被淘汰的页面被修改过时，才需要写回外存。因此，除了考虑一个页面最近有没有被访问过之外，操作系统还应考虑页面有没有被修改过。在其他条件都相同时，应优先淘汰没有修改过的页面，避免I/O操作。这就是改进型的时钟置换算法的思想。修改位=0，表示页面没有被修改过；修改位=1，表示页面被修改过。为方便讨论，用（访问位，修改位）的形式表示各页面状态。如（1，1）表示一个页面近期被访问过，且被修改过

设置为2个位优先淘汰没有被修改的页面

算法规则：

第一轮：从当前位置开始扫描到第一个（0，0）的帧用于替换。本轮扫描不修改任何标志位
第二轮：若第一轮扫描失败，则重新扫描，査找第一个（0，1）的帧用于替换。本轮将所有扫描过的帧访问位设为0
第三轮：若第二轮扫描失败，则重新扫描，查找第一个（0，0）的帧用于替换。本轮扫描不修改任何标志位
第四轮：若第三轮扫描失败，则重新扫描，査找第一个（0，1）的帧用于替换

由于第二轮已将所有帧的访问位设为0，因此经过第三轮、第四轮扫描定会有一个帧被选中，因此改进型 CLOCK置换算法选择一个淘汰页面最多会进行四轮扫描

一轮扫00 二轮扫01 三轮扫00 四轮扫01

操作系统之页面置换算法(三)

目录

操作系统之页面置换算法(三)

最佳置换算法(OPT)

先进先出算法 (FIFO)

最近最久未使用置换算法 (LRU)

时钟置换算法(CLOCK)

改进型的时钟置换算法

总结

Da Xin