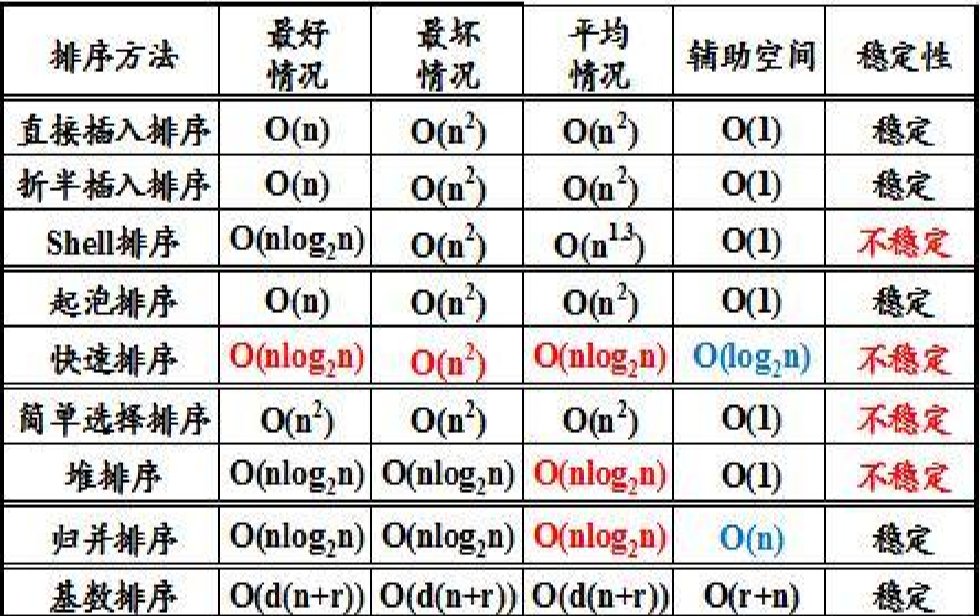
目录

排序算法

冒泡排序

基本流程: 第一个与第二个比 大交换 第二个与第三个比 大交换

public static void bubbleSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		for (int e = arr.length - 1; e > 0; e--) {
			for (int i = 0; i < e; i++) {
				if (arr[i] > arr[i + 1]) {
					swap(arr, i, i + 1);
				}
			}
		}
	}
	public static void swap(int[] arr, int i, int j) {
		arr[i] = arr[i] ^ arr[j];
		arr[j] = arr[i] ^ arr[j];
		arr[i] = arr[i] ^ arr[j];
	}

插入排序

基本流程: 从第2个数开始和第一个数比对,然后就是第3个数..

public static void insertionSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		for (int i = 1; i < arr.length; i++) {
			for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
				swap(arr, j, j + 1);
			}
		}
	}

	public static void swap(int[] arr, int i, int j) {
		arr[i] = arr[i] ^ arr[j];
		arr[j] = arr[i] ^ arr[j];
		arr[i] = arr[i] ^ arr[j];
	}

选择排序

基本流程:从第一个数开始 找到最小的下标,然后与第1个数进行交换 这时就确认第一个数是最小的,再从第二个数开始

public static void selectionSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		for (int i = 0; i < arr.length - 1; i++) {
			int minIndex = i;
			for (int j = i + 1; j < arr.length; j++) {
				minIndex = arr[j] < arr[minIndex] ? j : minIndex;
			}
			swap(arr, i, minIndex);
		}
	}

	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}

堆排序

非递归

2 * i + 1 : 左

2 * i + 2 : 右

(i - 1)/2 : 父

log1 + log2 + log3 + … log (n - 1) : O(N)

public static void heapSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		for (int i = 0; i < arr.length; i++) {
		// 进行堆的创建 堆是一个完全二叉树 而实质是一个数组
			heapInsert(arr, i);
		}
		int size = arr.length;
		swap(arr, 0, --size);
		while (size > 0) {
			heapify(arr, 0, size);
			swap(arr, 0, --size);
		}
	}

// 建立大/小 根堆时间复杂度为O(N) 调整只和完全二叉树的高度有关系
	public static void heapInsert(int[] arr, int index) {
	// 如果 父节点的值小于子节点 交换 并网上搜寻
		while (arr[index] > arr[(index - 1) / 2]) {
			swap(arr, index, (index - 1) / 2);
			index = (index - 1) / 2;
		}
	}
// 重新堆化 复杂度 O(logN)
	public static void heapify(int[] arr, int index, int size) {
	// 左边  size: 堆的边界 一个数组可能部分是堆
		int left = index * 2 + 1;
		while (left < size) {
		// left + 1 右孩子     largest找到了左右孩子中较大的那个
			int largest = left + 1 < size && arr[left + 1] > arr[left] ? left + 1 : left;
			// 和当前的再进行比较
			largest = arr[largest] > arr[index] ? largest : index;
			// 如果我仍是最大的 退出
			if (largest == index) {
				break;
			}
			// 不断往下沉
			swap(arr, largest, index);
			index = largest;
			left = index * 2 + 1;
		}
	}

	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}

递归

public static void heapSort(int[] array) {
  //初始堆，array[0]为第一趟值最大的元素
        array = buildMaxHeap(array); 
        for (int i = array.length - 1; i >= 1; i--) {
            //将堆顶元素和堆底元素交换，即得到当前最大元素正确的排序位置
            swap(array, 0, i);
            heapify(array, 0, i);  //整理，将剩余的元素整理成大顶堆
        }
    }

    //自下而上构建大顶堆：将array看成完全二叉树的顺序存储结构
    private static int[] buildMaxHeap(int[] array) {
        //从最后一个节点array.length-1的父节点（array.length-1-1）/2开始，直到根节点0，反复调整堆
        for (int i = (array.length - 2) / 2; i >= 0; i--) {
            heapify(array, i, array.length);
        }
        return array;

    }

    //自上而下调整大顶堆（递归）
    private static void heapify(int[] array, int k, int length) {
        int left = 2 * k + 1;
        if (left < length - 1 && array[left] < array[left + 1]) {
            left++;
        }
        if (left > length - 1 || array[k] >= array[left]) {
            return;
        } else {
            swap(array, k, left);
            heapify(array, left, length);
        }
    }

    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }

快速排序

递归

基本流程:比尾元素小的移动到序列左边，比尾元素大的移动到序列右边， 对以该元素为界的左右两个子序列（均不包括该元素）重复此操作 尾元素通过递归 是会改变的

public static void quickSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		quickSort(arr, 0, arr.length - 1);
	}

	public static void quickSort(int[] arr, int l, int r) {
		if (l < r) {
		// 随机选取一个作为哨兵 放于末尾
			swap(arr, l + (int) (Math.random() * (r - l + 1)), r);
			int[] p = partition(arr, l, r);
			quickSort(arr, l, p[0] - 1);
			quickSort(arr, p[1] + 1, r);
		}
	}
// 小于末尾的放左边 大于末尾的放右边 等于末尾的放中间
	public static int[] partition(int[] arr, int l, int r) {
		int less = l - 1;
		int more = r;
		while (l < more) {
			if (arr[l] < arr[r]) {
				swap(arr, ++less, l++);
			} else if (arr[l] > arr[r]) {
				swap(arr, --more, l);
			} else {
				l++;
			}
		}
		// 将刚开始的基准放到中间
		swap(arr, more, r);
		// 返回小于和大于的下标
		return new int[] { less + 1, more };
	}

	public static void swap(int[] arr, int i, int j) {
		int tmp = arr[i];
		arr[i] = arr[j];
		arr[j] = tmp;
	}

最坏时的情况就是 基准为序列中最大/小的元素 partition过程 一次是处理好一个元素 于是为O(n - 1 + n - 2 + .. + 1) = O(n^2)

非递归

public static void nonRecrutSort(int[] a) {
//非递归快排，两个栈 模拟递归调用
        //设置两个栈，一个用于保存
        if (a == null || a.length < 0) return;
        Stack<Integer> startStack = new Stack<Integer>();//保存当前划分的最高位
        Stack<Integer> endStack = new Stack<Integer>();//保存当前划分的最低位
        int start = 0;
        int end = a.length - 1;

        int pivotPos;

        startStack.push(start);
        endStack.push(end);

        while (!startStack.isEmpty()) {
            start = startStack.pop();
            end = endStack.pop();
            pivotPos = partition(a, start, end);
            if (start < pivotPos - 1) {
                startStack.push(start);
                endStack.push(pivotPos - 1);
            }
            if (end > pivotPos + 1) {
                startStack.push(pivotPos + 1);
                endStack.push(end);
            }
        }
    }

    public static int partition(int[] a, int start, int end) {//分块方法，在数组a中，对下标从start到end的数列进行划分
        int pivot = a[start];                     //把比pivot(初始的pivot=a[start]小的数移动到pivot的左边
        while (start < end) {                       //把比pivot大的数移动到pivot的右边
            while (start < end && a[end] >= pivot) end--;
            a[start] = a[end];
            while (start < end && a[start] <= pivot) start++;
            a[end] = a[start];
        }
        a[start] = pivot;
        return start;//返回划分后的pivot的位置
        //printArray(a);
    }
// 参考：http://blog.csdn.net/bnuside/article/details/6906688

归并排序

递归

分治法 划分一半左/右

	public static void mergeSort(int[] arr) {
		if (arr == null || arr.length < 2) {
			return;
		}
		mergeSort(arr, 0, arr.length - 1);
	}

	public static void mergeSort(int[] arr, int l, int r) {
		if (l == r) {
			return;
		}
		int mid = l + ((r - l) >> 1);
		mergeSort(arr, l, mid);
		mergeSort(arr, mid + 1, r);
		merge(arr, l, mid, r);
	}

	public static void merge(int[] arr, int l, int m, int r) {
		int[] help = new int[r - l + 1];
		int i = 0;
		int p1 = l;
		int p2 = m + 1;
		while (p1 <= m && p2 <= r) {
			help[i++] = arr[p1] < arr[p2] ? arr[p1++] : arr[p2++];
		}
		while (p1 <= m) {
			help[i++] = arr[p1++];
		}
		while (p2 <= r) {
			help[i++] = arr[p2++];
		}
		for (i = 0; i < help.length; i++) {
			arr[l + i] = help[i];
		}
	}

非递归

public static void MergeSort(int[] arr)
    {
        //使用非递归的方式来实现归并排序
        int len = arr.length;
        int k = 1;
        
        while(k < len)
        {
            MergePass(arr, k, len);
            k *= 2;         
        }
    }
    
    //MergePass方法负责将数组中的相邻的有k个元素的字序列进行归并
    private static void MergePass(int[] arr, int k, int n)
    {
        int i = 0;
        int j;
        
        //从前往后,将2个长度为k的子序列合并为1个
        while(i < n - 2*k + 1)
        {
            merge(arr, i, i + k-1, i + 2*k - 1);
            i += 2*k;
        }
        
        //这段代码保证了，将那些“落单的”长度不足两两merge的部分和前面merge起来。
        if(i < n - k )
        {
            merge(arr, i, i+k-1, n-1);
        }
        
    }
    
    //merge函数实际上是将两个有序数组合并成一个有序数组
    //因为数组有序，合并很简单，只要维护几个指针就可以了
    private static void merge(int[] arr, int low, int mid, int high)
    {
        //temp数组用于暂存合并的结果
        int[] temp = new int[high - low + 1];
        //左半边的指针
        int i = low;
        //右半边的指针
        int j = mid+1;
        //合并后数组的指针
        int k = 0;
        
        //将记录由小到大地放进temp数组
        for(; i <= mid && j <= high; k++)
        {
            if(arr[i] < arr[j])
                temp[k] = arr[i++];
            else
                temp[k] = arr[j++];
        }
        
        //接下来两个while循环是为了将剩余的（比另一边多出来的个数）放到temp数组中
        while(i <= mid)
            temp[k++] = arr[i++];
        
        while(j <= high)
            temp[k++] = arr[j++];
        
        //将temp数组中的元素写入到待排数组中
        for(int l = 0; l < temp.length; l++)
            arr[low + l] = temp[l];
    }
//  参考: https://www.jianshu.com/p/39dd1d9b491d

总结