目录
图
概述
- 无向图
- 有向图
- 加权图
- 加权有向图
Node:
public class Node {
public int value;
public int in;
public int out;
public ArrayList<Node> nexts;
public ArrayList<Edge> edges;
public Node(int value) {
this.value = value;
in = 0;
out = 0;
nexts = new ArrayList<>();
edges = new ArrayList<>();
}
}
Edge:
public class Edge {
// 权重
public int weight;
public Node from;
public Node to;
public Edge(int weight, Node from, Node to) {
this.weight = weight;
this.from = from;
this.to = to;
}
}
Graph:
public class Graph {
public HashMap<Integer,Node> nodes;
public HashSet<Edge> edges;
public Graph() {
nodes = new HashMap<>();
edges = new HashSet<>();
}
}
图的深度优先
public void dfs(Graph g, int v){
mark[v] =true;
for(int w:G.adj[v]){
if(!mark[w]){
// 这儿和上面的prev刚好反着来了
edgeTo[w] =v;
dfs(g,w);
}
}
}
// 将他标记为以访问 递归的访问它的所有没有被标记过的邻居节点 这里用栈来模拟
public static void dfs(Node node) {
if (node == null) {
return;
}
Stack<Node> stack = new Stack<>();
HashSet<Node> set = new HashSet<>();
stack.add(node);
set.add(node);
System.out.println(node.value);
while (!stack.isEmpty()) {
Node cur = stack.pop();
for (Node next : cur.nexts) {
if (!set.contains(next)) {
stack.push(cur);
stack.push(next);
set.add(next);
System.out.println(next.value);
break;
}
}
}
}
应用:
- 找出连通分量
无向图G的极大连通子图称为G的连通分量 任何连通图的连通分量只有一个,即是其自身
图的广度优先
public static void bfs(Node node) {
if (node == null) {
return;
}
Queue<Node> queue = new LinkedList<>();
HashSet<Node> map = new HashSet<>();
queue.add(node);
map.add(node);
while (!queue.isEmpty()) {
Node cur = queue.poll();
System.out.println(cur.value);
for (Node next : cur.nexts) {
if (!map.contains(next)) {
map.add(next);
queue.add(next);
}
}
}
}
// 广度优先搜索所需的时间再最坏的情况下和V+E成正比
对比二者
- 步骤都差不多
- 取出其中的下一个顶点并标记他
- 将v的所有相邻而又未被标记的顶点加入数据结构
- 取出下一个顶点的规则不一样(广度搜索是最早加入的顶点,深度优先搜索是最晚加入的顶点)
无向图
图是由一组顶点和一组能够将两个顶点相连的边组成的
概念介绍
- 图的密度: 已连接顶点对所有可能被连接的顶点对的比例
- 稀疏/稠密判定: 不同的边的数量是顶点数V的小的常数倍
- 连通图: 任意一个节点都能到达其他任何节点
- 多重图: 含有平行边的图
- 简单图: 无环或没有平行边的图
满足树的条件(任意一条即可):
- G有V-1条边且不含有环
- G有V-1条边且是联通的
- G是连通的,但删除任意一条边都会使它不再连通
- G是无环图,但添加任意一条边都会产生一条环
- G中的任意一对定点之间仅存在一条简单路径
api介绍

如何对上面的Api进行实现?
原则: 碰到的各种类型的图要有预留空间 实现方法要快
参考方案
- 领接矩阵: V^2 数组不能满足 且不能满足平行边
- 边的数组:不能实现adj() 求图的所有边
- 邻接表数组: 顶点数组,每个元素跟着一个链表
有向图
有向图和无向图没有多大的差别,只是有向图addEdge()时只添加一条边而已 即边是有方向的 头->尾
概念介绍
- 有向环:一条至少含有一条边且起点和终点相同的有向路径 有向图中的可达性和无向图中的连通性区别
- 出度: 该点指出的边的总数
- 入度: 指向该点的边的总数
解决问题
- 单点连通性
- 多点可达性
拓扑排序
给定一幅有向图,将所有的顶点排序,使得所有的有向边均从排在前面的元素指向排在后面的元素
- 拓扑序: 如果图中从ⅴ到w有一条有向路径,则v一定排在W之前。满足此条件的顶点序列称为一个拓扑序 获得一个拓扑序的过程就是拓扑排序
如果能够进行拓扑排序 一定是有向无环图(Directed Acyclic Graph, DAG)
一幅有向无环图的拓扑排序即为所有顶点的逆后序排列
public static List<Node> sortedTopology(Graph graph) {
HashMap<Node, Integer> inMap = new HashMap<>();
Queue<Node> zeroInQueue = new LinkedList<>();
for (Node node : graph.nodes.values()) {
inMap.put(node, node.in);
if (node.in == 0) {
zeroInQueue.add(node);
}
}
List<Node> result = new ArrayList<>();
while (!zeroInQueue.isEmpty()) {
Node cur = zeroInQueue.poll();
result.add(cur);
for (Node next : cur.nexts) {
inMap.put(next, inMap.get(next) - 1);
if (inMap.get(next) == 0) {
zeroInQueue.add(next);
}
}
}
return result;
}
顶点排序
基本思想:是深度优先搜索正好只会访问每个顶点一次 若将dfs()的参数顶点保存在一个数据结构(栈,队列)中 遍历这个数据结构就能访问途中的所有顶点 3种排列顺序:
- 先序: 递归调用前入队列
- 后序: 递归调用后入队列
- 逆后序: 递归调用后压入栈
有向图中的强连通性
强连通: 点v到点w和点w到点v是互相可达
强连通分量
- 自反性:任意顶点v和自己都是强连通的
- 对称性:如果v和w是强连通的,那么w和v也是强连通的
- 传递性:如果v和w是强连通的且w和x是强连通的,那么v和x也是强连通的
小结
| 问题 | 解决方案 |
|---|---|
| 单点和多点的可达性 | DirectedDFS |
| 单点有向路径 | DepthFirstDirectedPaths |
| 单点最短有向路径 | BreadthFirstDirectedPaths |
| 有向环的检测 | DirectedCycle |
| 深度优先的顶点排序 | DepthFirstOrder |
| 优先级限制下的调度问题/拓扑排序 | Topological |
| 强连通性 | KosarajuSCC |
| 顶点对的可达性 | TranitiveClosure |
最小生成树
无回路 且包含全部顶点 对于V个顶点 则一定有V - 1条边 边的权重和最小
概念介绍
加权图: 为每条边关联一个权值或是成本的图模型
生成树: 一棵含有其所有顶点的无环连接子图
最小生成树: 树中所有边的权值之和最小的树 连接无向图所有的点且没有环
最小生成森林: 非连通图 只能计算连通分量的最小生成树,合并在一起为最小生成森林
原理与定理
下面两条是证明的最小生成树的理论基础
- 用一条边连接树中的任意两个顶点都会产生一个新的环
- 从树中删去一条边将会得到两颗独立的树
- 切分定理: 将加权图分为两个集合,检查横跨两个集合的所有边并识别哪条边应属于图的最小生成树
- 加权图中,给定任意的切分,它的横切边中的权重最小者一定属于图的最小生成树
实现与表示
考虑到最小生成树是图的子图,同时根据名字也知道是一棵树,那么就有
- 一组边的列表
- 一幅加权无向图
- 一个以顶点为索引且含有父节点连接的数组
Prim算法
一开始这棵树只有一个顶点,每一步都会为一颗生长中的树添加一条边,然后会向它添加v-1条边,每次总是将下一条连接树中的顶点与不在树中的顶点且权重最小的边加入树中 (使用稠密图)
public static class EdgeComparator implements Comparator<Edge> {
@Override
public int compare(Edge o1, Edge o2) {
return o1.weight - o2.weight;
}
}
public static Set<Edge> primMST(Graph graph) {
// 优先级队列
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(
new EdgeComparator());
HashSet<Node> set = new HashSet<>();
Set<Edge> result = new HashSet<>();
for (Node node : graph.nodes.values()) {
if (!set.contains(node)) {
set.add(node);
// 将边放入优先级队列
for (Edge edge : node.edges) {
priorityQueue.add(edge);
}
while (!priorityQueue.isEmpty()) {
Edge edge = priorityQueue.poll();
// 边链接的顶点
Node toNode = edge.to;
if (!set.contains(toNode)) {
set.add(toNode);
result.add(edge);
// 继续将上面的链接toNode的边入队列
for (Edge nextEdge : toNode.edges) {
priorityQueue.add(nextEdge);
}
}
}
}
}
return result;
}
// 复杂度: T = O(|V|^2)
Kruskal算法
将森林合并成树(适用稀疏图) 非常直接了当的贪心,每次直接找权重最小的边,将他收进来,初始的情况,认为图中的每个顶点都是一棵树 然后把两颗树并成一棵树
public static class EdgeComparator implements Comparator<Edge> {
@Override
public int compare(Edge o1, Edge o2) {
return o1.weight - o2.weight;
}
}
public static Set<Edge> kruskalMST(Graph graph) {
// 准备一个并查集 因为是相当于不断扩这个地盘的 两个合并为1个地盘
UnionFind unionFind = new UnionFind();
// 让每个node都作为一棵树
unionFind.makeSets(graph.nodes.values());
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
// 将边全加入优先级队列中
for (Edge edge : graph.edges) {
priorityQueue.add(edge);
}
Set<Edge> result = new HashSet<>();
while (!priorityQueue.isEmpty()) {
Edge edge = priorityQueue.poll();
// from 和 to不是一棵树上的 不构成回路
if (!unionFind.isSameSet(edge.from, edge.to)) {
result.add(edge);
unionFind.union(edge.from, edge.to);
}
}
return result;
}
// 复杂度: T = O(|E|log|E|)
最短路径
Dijkstra算法
- 解决边权重非负的加权有向图的单起点的最短路径问题
- v个顶点E条边的加权有向图,所需空间与V成正比 时间与ElgV正比(最坏情况)
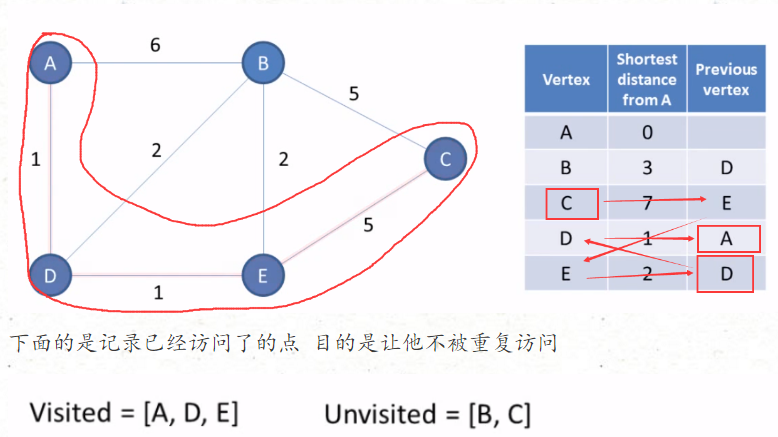
大致过程:设置起点为A, A->A 为0 再寻找与A直接连接的点 B D 这里看出来 D 的边值为 1 小于 B 的边值为 6 所以 选择D 继续探索 发现与D 直接相连的 点有 B 和 E 可根据之前的边值求得 A->B 的 路径和为 3 了 比之前的 6要小 那么就去更新 为 3 又 距离 A 点 最小的距离是 E 点 距离为 2 选择 E
Dijkstra算法算是一种贪心算法,已知最优解的情况 还是可以的
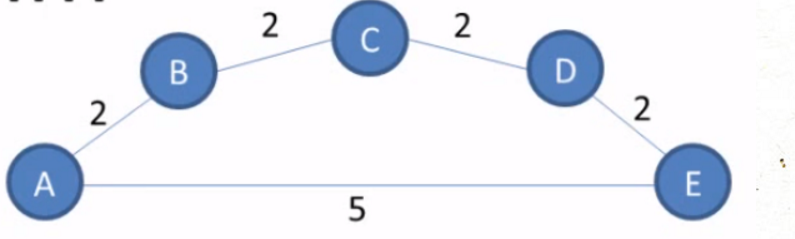
但碰到这种情况就比较的无奈了,刚好中了它的圈套
附加
Union-find 算法
union-find用于操作并查集这一数据结构
- Find:确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集
- Union:将两个子集合并成同一个集合
// Union-Find Set
public static class UnionFind {
private HashMap<Node, Node> fatherMap;
private HashMap<Node, Integer> rankMap;
public UnionFind() {
fatherMap = new HashMap<Node, Node>();
rankMap = new HashMap<Node, Integer>();
}
private Node findFather(Node n) {
Node father = fatherMap.get(n);
if (father != n) {
father = findFather(father);
}
fatherMap.put(n, father);
return father;
}
// 构造并查集
public void makeSets(Collection<Node> nodes) {
fatherMap.clear();
rankMap.clear();
for (Node node : nodes) {
fatherMap.put(node, node);
rankMap.put(node, 1);
}
}
public boolean isSameSet(Node a, Node b) {
return findFather(a) == findFather(b);
}
// 合并
public void union(Node a, Node b) {
if (a == null || b == null) {
return;
}
Node aFather = findFather(a);
Node bFather = findFather(b);
if (aFather != bFather) {
int aFrank = rankMap.get(aFather);
int bFrank = rankMap.get(bFather);
if (aFrank <= bFrank) {
fatherMap.put(aFather, bFather);
rankMap.put(bFather, aFrank + bFrank);
} else {
fatherMap.put(bFather, aFather);
rankMap.put(aFather, aFrank + bFrank);
}
}
}
}